Multifactor Dimensionality Reduction (MDR)
Method Description:
A multifactor dimensionality reduction (MDR) approach to detecting and characterizing high-order gene-gene interactions. A central problem in modeling interactions is the curse of dimensionality (Bellman 1961). That is, when high-order interactions are modeled, there are many contingency table cells (i.e. multilocus genotype combinations) that have no observations. In response to the limitation of traditional logistic regression for dealing with the curse or dimensionality, we have developed the multifactor dimensionality reduction (MDR) method for identifying gene-gene and gene-environment interaction effects on discrete clinical endpoints such as sporadic breast cancer (Ritchie et al. 2001; Moore and Williams 2002; Ritchie et al. 2003; Hahn and Moore 2003; Hahn et al. 2003). This data reduction approach seeks to identify combinations of multilocus genotypes and discrete environmental factors that are associated with high risk of disease and combinations that are associated with low risk. Thus, MDR defines a single variable that incorporates information from several loci and/or environmental factors that can be divided into high risk and low risk combinations. This new variable can be evaluated for its ability to classify and predict disease risk status using cross-validation (Hastie et al. 2001) and permutation testing (Good 2000). In the next several paragraphs, we describe the MDR approach.
MDR Figure
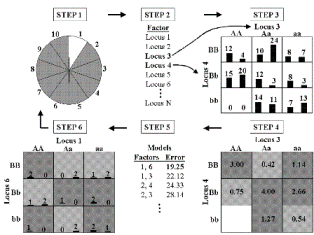
Figure 1 illustrates the general procedure involved in implementing the MDR method. In step one, the data are divided into a training set (e.g. 9/10 of the data) and an independent testing set (e.g. 1/10 of the data) as part of cross-validation (Hastie et al. 2001).
Second, a set of n genetic and/or environmental factors are selected. The n factors and their possible multifactor classes are represented in n-dimensional space; for example, for two loci with three genotypes each, there are nine possible two-locus-genotype combinations. Then, the ratio for the number of cases to the number of controls is calculated within each multifactor class. Each multifactor class in n-dimensional space is then labeled as “high risk” if the cases to controls ratio meets or exceeds some threshold (e.g. 1), or as “low risk” if that threshold is not exceeded; thus reducing the n-dimensional space to one dimension with two levels (“low risk” and “high risk”). Among all of the two factor combinations, a single model that has the fewest misclassified individuals is selected. This two-locus model will have the minimum classification error among the two locus models. In order to evaluate the predictive ability of the model, prediction error is estimated using 10-fold cross-validation. This entire procedure is performed ten times, using different random number seeds, to reduce the chance of observing spurious results due to chance divisions of the data.
For studies with more than two factors, the steps of the MDR method are repeated for each possible model size (2-factor, 3-factor, etc.), if computationally feasible. When not computationally feasible, machine learning strategies such as genetic algorithms (Goldberg 1989) can be employed. The result is a set of models, one for each model size considered. From this set, the model with the combination of loci and/or discrete environmental factors that maximizes the cross-validation consistency and minimizes the prediction error is selected. Cross-validation consistency is a measure of the number of times an MDR model is identified in each possible 9/10 of the subjects (Ritchie et al. 2001; Moore et al. 2002; Moore 2003). When cross-validation consistency is maximal for one model and prediction error is minimal for another model, statistical parsimony is used to choose the best model. Hypothesis testing of this final best model can then be performed by evaluating the magnitude of the cross-validation consistency and the prediction error. We determine statistical significance by comparing the cross-validation consistency and the prediction error from the observed data to the distribution of consistencies and prediction errors for the best models under the null hypothesis of no associations derived empirically from 1,000 or more permutations (Good 2000). The null hypothesis is rejected when the upper-tail Monte Carlo P-value derived from the permutation test is ? 0.05. The MDR approach is described in detail by Ritchie et al. (2001) and reviewed by Moore and Williams (2002). Ritchie et al. (2003) document the power of MDR to detect gene-gene interaction in the presence of genotyping error, missing data, phenocopy, and genetic heterogeneity. Hahn and Moore (2003) provide a formal proof that MDR ideally discriminates between discrete clinical endpoints using multilocus genotypes while Hahn et al. (2003) describe an initial MDR software package.
Related Publications:
- Ritchie, M.D., Hahn, L.W., Roodi, N., Bailey, L.R., Dupont, W.D., Plummer, W.D., Parl, F.F. and Moore, J.H. Multifactor Dimensionality Reduction Reveals High-Order Interactions among Estrogen Metabolism Genes in Sporadic Breast Cancer. American Journal of Human Genetics, 69:138-147. (2001)
- Hahn, L.W., Ritchie, M.D., and Moore, J.H. Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions. Bioinformatics, 19, 376-382. (2003).
- Ritchie, M.D., Hahn, L.W. and Moore, J.H. Power of multifactor dimensionality reduction for detecting gene-gene and gene-environment interactions. Genetic Epidemiology, 24, 150-157. (2003)
- Cho,Y.M., Ritchie, M.D., Moore, J.H., Moon, M.K., Lee, Y.Y, Yoon, K.H., Sung, Y.A., Lang, H.C., Park, J.Y., Lee, K.U., Shin, H.D., Kim, S.Y., Lee, H.K., Park, K.S. Multifactor Dimensionality Reduction Reveals a Two-Locus Interaction Associated with Type 2 Diabetes Mellitus. Diabetologia,47: 549-554 (2004).
- Tsai, C.T., Lai, L.P., Chiang, F.T., Fallin, D., Hwang, J.J., Ritchie, M.D., Moore, J.H., Hsu, K.L., Tseng, C.D., Liau, C.S., Lin, J.L., Tseng, Y.Z. Renin-Angiotensin System Gene Polymorphisms and Atrial Fibrillation. Circulation, 109: 1640-1646 (2004).
- Williams, S.M., Ritchie, M.D., Phillips, J.A., Wong, L.-J., Felder, R.A., Jose, P.A., Moore, J.H. Multilocus Analysis of Hypertension: A Hierarchical Approach, Human Heredity, 57:28-38 (2004).
- Coffey, C.S., Hebert, P.R., Ritchie, M.D., Krumholz, H.M., Morgan, T.M., Gaziano, J.M., Ridker, P.M., and Moore, J.H. An application of conditional logistic regression and multifactor dimensionality reduction for detecting gene-gene interactions on risk of myocardial infarction: The importance of model validation. BMC Bioinformatics, 5:49 (2004).
- Soares, M.L., Coelho, T., Sousa, A., Ritchie, M.D., Williams, S.M., Batalov, S., Conceição, I., de Lurdes, M., Luís, S., Saraiva , M.J., Buxbaum, J.N. Susceptibility and modifier genes in familial amyloid polyneuropathy type I. Human Molecular Genetics, in press
Related Links:
Computational Genetics Laboratory, Dartmouth – http://www.epistasis.org

